九月開學季,我梳理了給孩子們在課内學習、課外學習共七點建議。祝廣大學子們充分開展更多元的學習範式,提升自我的創新創造力!
我在《李開復給青少年的十二封信》書裏,也談過人工智能時代的教育,我覺得很適合在現在這個開學季再次分享給大家。比起應試考試中的分數,如果同學們具備“3C”的三大能力—— Curiosity(好奇心)、Critical thinking(批判式思維)、Creativity(創造力),未來更有可能實現自己的夢想。
■ 課內學習的4個建議:要充分利用好在學校裏上課的時間。
1. 要知其然,也要知其所以然
有同學問我:“怎樣學習知識,才能真正記住呢?每年考完試後,好像就把所有的知識還給老師了。”
我給這位同學的回答是:“我學懂的知識以及知道如何實踐的知識,我現在都還記得;在工作中常用的知識,我全部記得;我自己感興趣的知識,記憶更加清晰、準確,就算有不記得的,也可以快速推算出來;相反,那些靠死記硬背學到的知識,或者自己不感興趣的知識,我已經全忘掉了。”
也就是說,死記硬背只能過考試關,而不能獲取受益終生的知識。你們在學三角形面積定理時,一定都會背“底乘以高除以二”的公式。但是,你有沒有理解這個公式是如何推理出來的,為什麼三角形的面積是這樣計算的。記住這個公式和探索這個公式是如何推導出來的,學習的效果是不一樣的。有的同學學習化學,如果每天只是機械地背誦一些反應式,肯定會覺得枯燥無味,但如果掌握了每個反應式內在的規律,並能和現實中的化學現象聯繫起來,就會理解化學這門學科的意義所在,自然就會對這門學科產生興趣。
只有懂得了知識背後的道理,才能在遇到新的問題時舉一反三,才能在需要的時候,靈活地將自己掌握的知識付諸實踐。
2. 要多問問題
會提問也是一種能力,而且你也會因為提問而加深對問題的理解。
我的女兒在學習指數的時候,不理解指數是什麼,更不相信在真實生活中指數有什麼用處,就主動來問我。我用計算銀行存款的思路來指導她,比如存入 100 元,每年的利息是 10%,那麼 10 年後,你的存款是多少?
通過這樣的計算,她終於明白了,原來指數知識和日常生活息息相關。而她能得到對這個問題的認識,也是因為她主動提問獲得的。
多提一個問題,你就擁有一種多瞭解這個世界的可能性。只有不懂就問,才能真正學到有用的知識。
3. 要勤奮
能夠實現自己的夢想的人,一定是勤奮的。
去美國讀中學之前,我只學過半年英語,因此,語言障礙成為我面臨的最大難關。剛開始,同學和老師說的話,我幾乎一句也聽不懂,那種感覺非常痛苦。那“催眠”一般的語速,總讓我在課堂上打起瞌睡。有時候,聽到同學們因為老師的一句笑話笑得前仰後合,我才從夢中驚醒,但還是摸不著頭腦。天書一般的英文,開始讓我有些望而卻步,後來,我乾脆帶幾本中文的武俠小說到課上去讀,因為覺得怎麼聽也聽不懂,還不如看小說。
然而,我心裏又是暗暗憋了一股勁的。於是,我找了一大本英文單詞書來背,經常背到半夜,不會的就一次次地翻厚厚的中英對照詞典。不過,沒多久,我就發現這並不是學英文的最好方法。因為,即使當時記住了一個單詞,但是使用率不高的話,就會完全忘記。我終於悟到了,在沒有語境的情況下,背單詞是沒用的。
後來,我還是下定決心用多交流的方式來學習英文。下了課,我不再膽怯,站在同學中間聽他們說話。如果 5個詞當中有 4個聽懂了,只有一個聽不懂,我也會趕緊問,同學們會再用英文解釋一遍給我聽。回家以後,我會默默回憶我聽不懂的單詞,然後記下來。而上課的時候,遇到聽不懂的內容,我也勇敢舉手問老師,請求老師再說一遍。
我遇到了一位好老師,她甚至犧牲自己的午飯時間幫我一對一地補習英文,她複印了小學一年級的課文,每天拿來給我念。從簡單的課文起步,我們堅持了一年。在這一年裏,我的英文水平迅速提高。學校裏所有的老師還允許我享受“開卷考試”的特殊待遇,她們讓我把試卷帶回家,並且告訴我題目裏不認識的單詞可以查字典,但是不能看書找答案。我每次回到家都嚴格按照老師說的做,遇到題目裏不認識的單詞就去查字典,但是從來沒有去翻書找過答案。因為,我覺得這是老師給我的最大信任,我不能辜負這份信任。
通過種種渠道的學習,我的英文終於逐漸接近同齡人的水平了。一年以後,我完全可以聽懂老師講的話了,英文會話也沒有問題了。到了初中三年級,也就是到美國兩年之後,我寫的作文居然獲得了田納西州的前十名。我想,這和我年齡小,容易接受新的語言不無關係,但也和我勤奮的學習有關。
4. 要培養獨立思考的能力
我在人生的各個階段,都獲益於獨立思考的能力。甚至想不到的是,這種批判式的獨立思考的能力,“救”了我的命。
在我五十二歲生日前不久,我在一次體檢中被查出肚子裏有數十顆“腫瘤”,經過反復復查,我被醫生宣判得了第四期淋巴癌。在毫無防備的情況下,我突然感受到死神和自己離得那麼近;我氣餒、懊悔、內疚,但是,治療過程中的一件具有轉折意義的事件發生了。
我遇到了一個好醫生。我的主治醫生唐季祿給我打氣:“淋巴癌第四期真的沒那麼嚴重,它跟肝癌、肺癌第四期是不太一樣的。”他告訴我,網絡上有兩篇專門討論“濾泡性淋巴癌存活率的預估方式”的論文,如果我有興趣,可以找出來看看。我認真地研究了唐醫生推薦的那些學術文章,發現淋巴癌的分期方式已經有四十多年了,可以說過時且不精准了。如果說只看標準的分類,我因為腫瘤數太多,所以必須歸類為第四期。但是只看腫瘤數量是最準確的嗎?根據我研究的那幾篇論文,分期的目的就是預測存活概率和時間。那麼,最準確的預測方法就是尋找和我病情足夠相似的人,根據他們的不同因素,如年齡、症狀、血液指數、腫瘤數量及大小等 20多種,和他們的實際存活結局來理解哪些因素是最重要的,並且把這些因素整合起來。這樣的研究肯定要比四十多年前的粗分類來得准!
自己研究病情,就像是自己坐在副駕駛座上,可以隨時掌握路況。醫生的治病策略、用藥思維,你至少並不是茫然無知。我又拿出以前做學術的精神,把全部20幾個特徵與我的檢查結果相對照,發現我雖然屬於第四期,但整體狀況其實沒那麼悲觀。原來醫學上對所有淋巴癌的分期方式,至少對我的病情來說是不正確的,我的情況是較輕的。於是,我突然從“第四期癌症頂多幾個月”,變成“至少還有好幾年”可以活。倘若好好照顧自己,更有可能終身不再復發!這個發現有如一線曙光,從此之後,癌症所帶來的一切負面影響,就開始悄悄起了變化。
批判性地看待醫學上對淋巴癌的分類,通過獨立思考,獨立研究的方式來獲得對自己病情的準確判斷,讓我自己從精神上獲得了新生。
■ 課外學習的3個建議:課堂外的時間,我鼓勵同學們,去探索你們熱愛的東西,多實踐,多多鍛煉自己的創造力。
5. 要動手實踐
美國華盛頓兒童博物館的牆上寫了這樣一句格言:“我聽到的會忘掉,我看到的能記住,我做過的才真正明白。”
我記得小時候,我的父親曾讓我們幾個兄弟姐妹解答這樣一個問題:用 6 根火柴拼成 4 個大小一模一樣的正三角形。通過動手實踐,我們都找到了正確的答案。這樣的實踐讓我對相關的幾何和空間知識記憶深刻,也訓練了我使用新穎的思維解決問題的能力。
我在高中時參與美國的高中生創業嘗試課程,創辦自己的公司。我們當時的公司非常簡單,就是從當地的建材市場買來鋼材,然後利用週末時間到工廠裏加工這些鋼材,我們把鋼材切成很小的一塊塊圓環,然後在圓環上刻上簡單的雕花。在負責推廣的過程中,我們發現學生的家長並不需要這樣的圓環,最後產品幾乎是內部消化掉了。
這次的親身實踐,讓當時 15 歲的我意識到,真正好的產品,不是求人去買的,而是必須有市場需求。有了這樣的認識,我在第二次的創業嘗試中就會把市場需求作為我創辦的公司的方向。從需求出發,生產有需求的產品,牢記這樣的理念,第二次的創業嘗試獲得了成功。這些對於創辦公司的經驗,都是我從實踐中一點一滴積累起來的。
只有實踐,你才能知道你的想法是否可行。
6. 要追隨自己的興趣愛好
只有做自己真正喜歡做的事情,才能做到最好。
我在上大學時,一直以為自己喜歡法律,將來想做一名律師。可是上了幾門課後,我發現自己對此毫無興趣,於是跟家人商量轉系,數學是我的一個備選項。但是,當我加入了“數學天才班”後,發現我的數學突然從“最好的”變成“最差的”。我雖是田納西州的冠軍,但當我與來自加州或紐約的“數學天才”交手時,才發現自己真的技不如人。我深深地體會到那些數學天才是因為“數學之美”而對它癡迷的,而我並非如此。我一方面羡慕他們找到了最愛,一方面遺憾自己並不是真的數學天才,也不會為了它的美而癡迷,因為我不希望我的人生意義就是為了理解數學之美。
我想到了計算機,我在高中時就對計算機有濃厚的興趣,有一次,為了解答一個複雜的數學方程式,我寫了一個程式,然後把結果打印出來。當時因為機器運行的速度太慢,我沒有等到結果打印出來就回去了。週一回到學校,我才知道我們學校所有的打印紙都被我打光了。雖然挨了老師一通罵,但我的心裏有了一股欣喜,原來這個數學方程式有無數的解,我走後,程式一直在運行,計算機就一直在打印結果。
對計算機的興趣此時在我的心中醞釀,雖然當時計算機專業算是個默默無聞的專業。接下來,我選修了一門計算機編程課,幾個月的課上下來,我發現了自己在計算機方面的天賦。我和同學們一起做編程,他們還在畫流程圖,我就已經完成了所有的題目。考試的時候,我比別人交卷的時間幾乎早了一半,我不用特別準備,也能拿高分。
通過學習計算機 , 我有了一種前所未有的震撼:未來這種技術能夠思考嗎?它能夠讓人類更有效率嗎?計算機有一天會取代人腦嗎?我感受到了一種振奮,解決這樣的問題是我一生的意義所在。
我每天都像海綿一樣吸收著知識,在一門公認為是計算機專業最難通過的“可計算性和形式語言”課上,我考了 100 分,也就是A+ 的分數,創造了該系的一個紀錄。大三大四時我就開始和研究生一起選修碩士和博士課程,接手各式各樣的項目,在這些項目中,我嘗試著攻克一個又一個的難關。畢業後,我在計算機方面創造出了一些成果。
我覺得自己是幸運的,因為我在很年輕的時候,就找到了自己熱愛的事情,並且願意為之付出一生的努力。
7. 要多培養自己的創造力
我的中學是在美國的橡樹嶺讀的,當時的感受就是,學校的功課很輕鬆,每天的家庭作業很少,但是每天有很多稀奇古怪的項目。比如,當時歷史課教到美國印第安人的時候,不是用課本告訴你發生了什麼,而是讓一個團隊寫一個話劇,或者是進行關於移民者和印第安人的辯論。
這些項目都沒有一個標準的答案,但會引導我們從不同的角度看問題,但我們的創造力和想像力,可以在這些稀奇古怪的題目中得到鍛煉。
後來,我回到北京創辦微軟中國研究院面試時,對前來面試的學生也注重的是對他們思維方式的考驗,我們向面試者提出了這樣的問題:
o 為什麼下水道的蓋子是圓形的?
o 估計一下北京一共有多少個加油站。
o 你和你的導師如果發生分歧怎麼辦?
o 給你一個非常困難的問題,你想怎樣去解決它?
o 兩條不規則的繩子,每條繩子的燃燒時間為 1小時,請在 45分鐘燒完兩條繩子。
這些題目雖然聽上去很“怪”,但我們出題的本質也不一定要聽到正確答案,而是要從回答問題的思路中聽到面試者的思維方法。
孩子們,比起試卷上的分數,我認為你們底層的思維能力,會是更珍貴的能力。你在學習每一門科目時,鍛煉出來的能力是未來最能幫助你們的事情。就像你學了代數,也許不會去研究數學,但是這對鍛煉你的思維有幫助;你學了英文,不一定會出國,但是英文可以在瞭解世界最前沿的文獻、在有效交流方面幫助你;你學了畫畫,不一定成為畫家,但是你在學習畫畫的過程中鍛煉的觀察力、空間力、想像力會對你有幫助。
過去,我們對教育成功的衡量標準是學生能不能記得被教的東西。但是未來,教育的精華體現在即使你忘記了所有你學的東西,你還具備思維方式、智慧和能力。
當你已經忘記了歷史事件發生的年代,你還是知道歷史帶給我們的人類的智慧和教訓;當你已經不會編程了,你還是有編程帶給你的邏輯思維;當你已經不會背莎士比亞的詩了,你依然懂得文學的美,這些才是教育的精華。
同時也有22部Youtube影片,追蹤數超過11萬的網紅GreatKidsLearning,也在其Youtube影片中提到,利用等腰三角形性質、畢氏定理、三角形面積公式來解題 歡迎大家加入會員,贊助此影音頻道...
「三角形面積」的推薦目錄:
- 關於三角形面積 在 Facebook 的最佳貼文
- 關於三角形面積 在 偉傑英數 Facebook 的最佳解答
- 關於三角形面積 在 寶妮老師 Charming Teacher Bonnie Facebook 的精選貼文
- 關於三角形面積 在 GreatKidsLearning Youtube 的精選貼文
- 關於三角形面積 在 GreatKidsLearning Youtube 的精選貼文
- 關於三角形面積 在 寶妮老師 Bonnie Youtube 的最佳解答
- 關於三角形面積 在 [問題] 還有... >.< - 精華區tutor 的評價
- 關於三角形面積 在 陳易數學- #利用外接圓半徑求三角形面積#外心 ... - Facebook 的評價
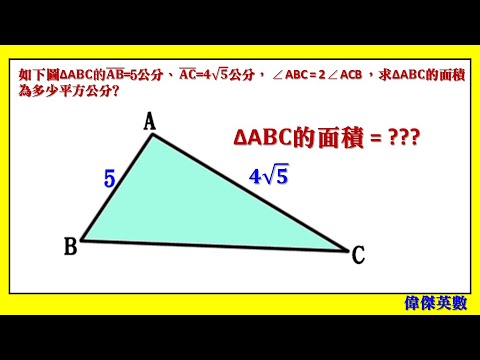
三角形面積 在 偉傑英數 Facebook 的最佳解答
利用等腰三角形性質、畢氏定理、三角形面積公式來解題
請參考影片解題: https://www.youtube.com/watch?v=hK-t1NgerzU
三角形面積 在 寶妮老師 Charming Teacher Bonnie Facebook 的精選貼文
中二病發作🤷🏻♀️
不過面積公式還是要認真學
今天晚上九點
一起來練習三角形之呼吸吧💪💪💪
#鬼滅之刃 #炎柱 #三角形 #面積 #全集中の呼吸 #全集中 #水之呼吸 #數學筆記 #煉獄杏壽郎 #大哥沒有輸
三角形面積 在 寶妮老師 Bonnie Youtube 的最佳解答
每次碰到求面積都很苦惱嗎:)
快跟寶妮一起來看看
高中可以用哪些方法求面積吧
........................................
抖內連結:
https://p.ecpay.com.tw/04FD83A
........................................
Hello!我是Bonnie,大家最害怕的高中數學老師。
因為有感於現今網路多媒體遠比課本紙筆更有吸引力,所以決定除了在學校之外,也在網路上分享我的生活、教學、自修以及與學生相處的小心得。
如果你還是學生,你可以發現老師其實沒那麼討人厭😂如果你已經畢業,你可以在這裡找回一點青春回憶👩🎓👨🎓
Enjoy it and have a good time!
.........................................
IG: charmingteacherbonnie (Bonnie老師)
粉絲專頁: 寶妮老師
https://www.facebook.com/%E5%AF%B6%E5%A6%AE%E8%80%81%E5%B8%AB-Charming-Teacher-Bonnie-290462364959770/

三角形面積 在 陳易數學- #利用外接圓半徑求三角形面積#外心 ... - Facebook 的推薦與評價
利用外接圓半徑求三角形面積#外心#外接圓#陳易數學#公式懶人包#懶人公式包. ... <看更多>






三角形面積 在 [問題] 還有... >.< - 精華區tutor 的推薦與評價
1 給三高,如何求三角形面積ㄚ?
2 給三邊長,求此三角形三中線長所圍成的三角形面積...
(AB=4,BC=5,AC=5)
--
※ 發信站: 批踢踢實業坊(ptt.csie.ntu.edu.tw)
◆ From: 140.112.84.54
> -------------------------------------------------------------------------- <
作者: rath (出手便知有沒有) 看板: tutor
標題: Re: [問題] 還有... >.<
時間: Sun Dec 22 12:48:49 2002
※ 引述《timmy (呆 子..)》之銘言:
: 1 給三高,如何求三角形面積ㄚ?
假設三高為 2,3,6
則三邊長比為 1/2 : 1/3 : 1/6 = 3 : 2 :1
所以三邊長為 3k ,2k , k
利用三邊長的海龍公式=某一邊得底乘高 即可得
: 2 給三邊長,求此三角形三中線長所圍成的三角形面積...
: (AB=4,BC=5,AC=5)
三中線圍不出三角形喔同學
--
렠 任思緒飛揚,隨筆而至ꄊ
--
※ 發信站: 批踢踢實業坊(ptt.csie.ntu.edu.tw)
◆ From: 210.85.79.52
> -------------------------------------------------------------------------- <
作者: doa2 (單身族耶誕夜烤) 看板: tutor
標題: Re: [問題] 還有... >.<
時間: Sun Dec 22 14:13:09 2002
※ 引述《rath (出手便知有沒有)》之銘言:
: ※ 引述《timmy (呆 子..)》之銘言:
: : 1 給三高,如何求三角形面積ㄚ?
: 假設三高為 2,3,6
: 則三邊長比為 1/2 : 1/3 : 1/6 = 3 : 2 :1
: 所以三邊長為 3k ,2k , k
: 利用三邊長的海龍公式=某一邊得底乘高 即可得
: : 2 給三邊長,求此三角形三中線長所圍成的三角形面積...
^^^^
應該算出三中線長
用海龍公式就可
: : (AB=4,BC=5,AC=5)
: 三中線圍不出三角形喔同學
--
※ 發信站: 批踢踢實業坊(ptt.csie.ntu.edu.tw)
◆ From: 140.112.249.46
> -------------------------------------------------------------------------- <
作者: Triheart (Locked Aeolus) 看板: tutor
標題: Re: [問題] 還有... >.<
時間: Sun Dec 22 14:50:17 2002
※ 引述《timmy (呆 子..)》之銘言:
: 1 給三高,如何求三角形面積ㄚ?
前面有人解過了
: 2 給三邊長,求此三角形三中線長所圍成的三角形面積...
: (AB=4,BC=5,AC=5)
你隨便延伸一邊的中線之後畫出一個對稱三角形
上下的三角形會被各自的中線各切成六塊面積相等的小三角
其中由上下兩塊小的合起來的三角形三邊長分別是2/3中線長 (麻煩自己找)
所以由2/3中線長圍成的三角形面積是原三角形的 2/6
所以中線長圍成的三角形面積 = 原三角形面積 x 2/6 x 9/4 (相似形)
原三角面積不用我求了吧? (既然是等腰我會先求高)
至於前面問的那題
1 三角形ABC中,BC=7,AC=5,AB=3
求角平分線 AD=?
3.5.7一看就知道是A=120度的三角形啊 解釋給學生聽可用餘弦
這一看就知道是120度的角平分線長求法啊 果然他問的是A的角平分線
幹嘛要求什麼BD... 就算背公式也知道 1/AD = 1/AB + 1/AC
學生還不知道為什麼的話 再用面積公式去證明該式就好了...
-----------------------------------------------------------------
這些題目都蠻基本的 我會三不五十在不同地方就跟學生重提 ^^
當然用海龍也可以解 看個人喜好囉... 我是很懶得算根號啦
--
.
. 定 格 .
.
--
※ 發信站: 批踢踢實業坊(ptt.csie.ntu.edu.tw)
◆ From: 140.112.212.12
> -------------------------------------------------------------------------- <
作者: coco1003 (小精靈) 看板: tutor
標題: Re: [問題] 還有... >.<
時間: Sun Dec 22 14:57:40 2002
※ 引述《Triheart (Locked Aeolus)》之銘言:
: ※ 引述《timmy (呆 子..)》之銘言:
: : 1 給三高,如何求三角形面積ㄚ?
: 前面有人解過了
: : 2 給三邊長,求此三角形三中線長所圍成的三角形面積...
: : (AB=4,BC=5,AC=5)
: 你隨便延伸一邊的中線之後畫出一個對稱三角形
: 上下的三角形會被各自的中線各切成六塊面積相等的小三角
: 其中由上下兩塊小的合起來的三角形三邊長分別是2/3中線長 (麻煩自己找)
: 所以由2/3中線長圍成的三角形面積是原三角形的 2/6
: 所以中線長圍成的三角形面積 = 原三角形面積 x 2/6 x 9/4 (相似形)
: 原三角面積不用我求了吧? (既然是等腰我會先求高)
: 至於前面問的那題
: 1 三角形ABC中,BC=7,AC=5,AB=3
: 求角平分線 AD=?
: 3.5.7一看就知道是A=120度的三角形啊 解釋給學生聽可用餘弦
: 這一看就知道是120度的角平分線長求法啊 果然他問的是A的角平分線
: 幹嘛要求什麼BD... 就算背公式也知道 1/AD = 1/AB + 1/AC
: 學生還不知道為什麼的話 再用面積公式去證明該式就好了...
: -----------------------------------------------------------------
: 這些題目都蠻基本的 我會三不五十在不同地方就跟學生重提 ^^
: 當然用海龍也可以解 看個人喜好囉... 我是很懶得算根號啦
哇......
好多漸漸被遺忘的東西喔...
請問一下...
這是國三上的東西嗎???
--
※ 發信站: 批踢踢實業坊(ptt.csie.ntu.edu.tw)
◆ From: 61.70.151.17
> -------------------------------------------------------------------------- <
作者: Welin (依然深愛你...) 看板: tutor
標題: Re: [問題] 還有... >.<
時間: Sun Dec 22 15:57:55 2002
※ 引述《doa2 (單身族耶誕夜烤)》之銘言:
: ※ 引述《rath (出手便知有沒有)》之銘言:
: : 假設三高為 2,3,6
: : 則三邊長比為 1/2 : 1/3 : 1/6 = 3 : 2 :1
: : 所以三邊長為 3k ,2k , k
: : 利用三邊長的海龍公式=某一邊得底乘高 即可得
: ^^^^
: 應該算出三中線長
: 用海龍公式就可
: : 三中線圍不出三角形喔同學
海龍公式現在的國中數學課本已經沒有了~
我國中的時候會學到海龍公式是因為補習太混
被老師抓去寫講義才學到的....
--
愛是一種感覺,即使痛苦也覺得幸福;
愛是一種體會,即使心碎也覺得甜蜜;
愛是一種經驗,即使破碎也覺得美麗!
--
※ 發信站: 批踢踢實業坊(ptt.csie.ntu.edu.tw)
◆ From: 61.217.228.35
> -------------------------------------------------------------------------- <
作者: rath (出手便知有沒有) 看板: tutor
標題: Re: [問題] 還有... >.<
時間: Sun Dec 22 17:33:00 2002
※ 引述《Triheart (Locked Aeolus)》之銘言:
: ※ 引述《timmy (呆 子..)》之銘言:
: : 1 給三高,如何求三角形面積ㄚ?
: 前面有人解過了
: : 2 給三邊長,求此三角形三中線長所圍成的三角形面積...
: : (AB=4,BC=5,AC=5)
: 你隨便延伸一邊的中線之後畫出一個對稱三角形
: 上下的三角形會被各自的中線各切成六塊面積相等的小三角
: 其中由上下兩塊小的合起來的三角形三邊長分別是2/3中線長 (麻煩自己找)
: 所以由2/3中線長圍成的三角形面積是原三角形的 2/6
: 所以中線長圍成的三角形面積 = 原三角形面積 x 2/6 x 9/4 (相似形)
: 原三角面積不用我求了吧? (既然是等腰我會先求高)
: 至於前面問的那題
: 1 三角形ABC中,BC=7,AC=5,AB=3
: 求角平分線 AD=?
: 3.5.7一看就知道是A=120度的三角形啊 解釋給學生聽可用餘弦
: 這一看就知道是120度的角平分線長求法啊 果然他問的是A的角平分線
: 幹嘛要求什麼BD... 就算背公式也知道 1/AD = 1/AB + 1/AC
: 學生還不知道為什麼的話 再用面積公式去證明該式就好了...
: -----------------------------------------------------------------
: 這些題目都蠻基本的 我會三不五十在不同地方就跟學生重提 ^^
: 當然用海龍也可以解 看個人喜好囉... 我是很懶得算根號啦
if not?
如果求角B呢
又或者求三角形內"任意一條"線呢?
特別的做法也許精采
但是一般的做法我想對學生幫助更大
還有啊 你的公式只能用在角A是120度的時候
如果角A是60度呢?
更遑論連角A度數不給你都可以做出來角平分線了
給學生魚吃不如教他怎麼釣魚
共勉 ^^
--
렠 任思緒飛揚,隨筆而至ꄊ
--
※ 發信站: 批踢踢實業坊(ptt.csie.ntu.edu.tw)
◆ From: 210.85.79.52
※ 編輯: rath 來自: 210.85.79.52 (12/22 17:36)
> -------------------------------------------------------------------------- <
作者: Triheart (Locked Aeolus) 看板: tutor
標題: Re: [問題] 還有... >.<
時間: Sun Dec 22 18:49:38 2002
※ 引述《rath (出手便知有沒有)》之銘言:
: if not?
: 如果求角B呢
: 又或者求三角形內"任意一條"線呢?
如果這個題目不是3.5.7 不是120度 我自然不會這麼做
但是這個題目之所以出現在書本裡 通常是搭配著這個範圍的內容而設計
有興趣的人不妨翻一下參考書
在證明120度角的平分線公式時常搭配著3.5.7這個三角形
: 特別的做法也許精采
: 但是一般的做法我想對學生幫助更大
: 還有啊 你的公式只能用在角A是120度的時候
: 如果角A是60度呢?
求角平分線長度的題目常見的角度是120度,90度,60度
我想有些參考書有整理這部分的題型
其結果都是類似的 k/AD = 1/AB + 1/AC 其中的k隨角度不同而變化
我曾經教過的一個學生 把角度跟k值背下來 卻不知其所以然
我當時是建議他用面積來想 1/2 b x c x sin A
用兩倍角之後消去sin A/2
餘下的cos A/2若是特別角 這個題目就有個漂亮的k
也就是因此 120度,90度,60度是常見的題型
這是我高中時學習 以及當家教時常看到的寫法
我不知道是不是有什麼版本的書沒有提 ?
還是教材更新時刪掉了?
: 更遑論連角A度數不給你都可以做出來角平分線了
: 給學生魚吃不如教他怎麼釣魚
: 共勉 ^^
我並不認為題目給了三邊之後 求角度是一件麻煩的事情
尤其是3.5.7這種出現頻率相當高的三角形 找出120度之後沒那麼神奇了
我不會覺得我的方法是無懈可擊的
我會提供各種方法 包括各位的方法給我的學生
然後再讓他想想喜歡用哪種方法
我給的就是建議而已
不同的學校上的方法各有不同
比如我正在教的兩個不同校但同年級的學生
如果要他們求過三點的平面方程式
他們一個會用外積做 另一個會用行列式做
如果要他們做點到平面的投影點
一個會用k的公式解 另一個會用直線參數式
方法各有巧妙不同 我覺得輔助學生找到最順手(or順腦)的方法很重要
我也不會把公式認為是不好的 :p
只要清楚公式內涵 有很多東西是相當有利的工具~
實際上數學要背誦的東西原本就不多 ...
我會鼓勵學生背一些實用的
如果他們背不起來 我至少也會讓他們學一個最基本的解法 即使是土法煉鋼
繼續共勉 :)
--
.
. 定 格 .
.
--
※ 發信站: 批踢踢實業坊(ptt.csie.ntu.edu.tw)
◆ From: 140.112.212.12
... <看更多>